Справочник Бухгалтера

Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.

Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.

Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.

Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.

Расчет текущей стоимости (PV) серии равных денежных потоков.

Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при t = 1).

Всего простой аннуитет включает N платежей с первым взносом при t = 1 и последним при t = N.

Мы можем выразить текущую (приведенную) стоимость обычного аннуитета как совокупность текущей стоимости каждого отдельного аннуитетного платежа, как указано ниже:

\( \mathbf {PV = {A \over (1 + r)} + {A \over (1 + r) ^ 2} + {A \over (1 + r) ^ 3} + \cdots + {A \over (1 + r)^{N-1}} + {A \over (1 + r)^N}} \) (формула 10)

где:

• A = сумма аннуитета,
• r = процентная ставка за период, соответствующая частоте выплаты аннуитета (например, годовой, ежеквартальный или ежемесячный),
• N = количество аннуитетных платежей.

Поскольку аннуитетный платеж (A) является константой в этом уравнении, его можно вывести за скобки. Таким образом, это выражение можно привести к следующей формуле:

\( \mathbf {PV = A \left } \) (формула 11)

Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим текущую стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в формуле 11.

Пример расчета текущей (приведенной) стоимости обычного аннуитета.

Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1 000 каждый год в течение 5 лет с первым платежом через год.

Норма прибыли составляет 12% в год.

Сколько вы должны заплатить за этот актив?

Решение:

Чтобы узнать стоимость финансового актива, используйте формулу (11) текущей стоимости обычного аннуитета, со следующими данными:

A = €1,000
r = 12% = 0.12
N = 5

\( \mathbf { \begin{aligned} PV &= A \left \\ &= €1 \ 000 \left \end{aligned} } \)

= €1,000 * (3.604776)
= €3,604.78

Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.

Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).

При авансовом аннуитете 1-ый платеж выполняется в текущую дату (t = 0). В общей сложности авансовый аннуитет включает N платежей.

На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.

Авансовый аннуитет в размере $100 за период.

На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:

• единовременная сумма в размере $100 на текущую дату (при t = 0) и
• обычный аннуитет в размере $100 за период в течение 3-х периодов.

При ставке дисконтирования в 12% четыре денежных потока в размере 100$ в этом примере авансового аннуитета будут стоить $340,18.

Существует альтернативный способ расчета текущей стоимости авансового аннуитета.

По сравнению с обычным аннуитетом каждый платеж авансового аннуитета дисконтируется на 1 период раньше.

Поэтому мы можем модифицировать формулу 11, умножив правую часть уравнения на (1 + r):

PV (Авансовый аннуитет) = \( \mathbf {A \left (1+r) } \)

Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.

Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.

Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.

Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:

• немедленную единовременную выплату в размере $2 млн. или
• аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.

Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.

Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.)

Решение:

Чтобы сравнить эти два варианта, необходимо найти текущую стоимость каждого из них в момент времени
t = 0 и выбрать наибольшее значение.

Текущая стоимость первого варианта составляет $2 млн., т.е. первый вариант уже выражен в сегодняшнем эквиваленте.

Второй вариант — аннуитет. Поскольку первый платеж происходит при t = 0, вы можете разделить этот аннуитет на две части:

• немедленную выплату $200 000 от текущей даты (t = 0) и
• обычный аннуитет в размере $200 000 в год в течение 19 лет.

Чтобы рассчитать этот аннуитет, вам нужно найти текущую стоимость обычного аннуитета, используя формулу 11, а затем добавить к нему 200 000 долларов.

A = $200,000
N = 19
r = 7% = 0.07

19 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.

Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.

Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.

Пример расчета прогнозируемой текущей стоимости обычного аннуитета.

Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при t = 10.

После того, как пособия начнут выплачиваться, эти выплаты продлятся до t = 39, что составляет в общей сложности 30 платежей.

Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионному плану составляет 5% годовых, начисляемых ежегодно?

Решение:

Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при t = 10.

При этом, на момент t = 9 мы имеем обычный аннуитет с 30 платежами. Мы можем вычислить текущую стоимость (PV) этого аннуитета с помощью формулы 11, а затем посмотреть на нее на временной шкале.

A = €1,000,000
r = 5% = 0.05
N = 30

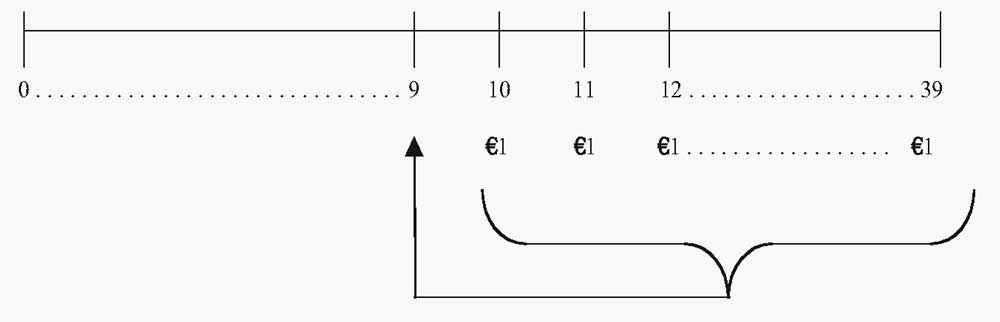Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).

На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от t = 10 до t = 39.

Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени t = 9.

Текущая стоимость (PV) пенсионных пособий по состоянию на t = 9 составляет €15,372,451.03.

Далее задача заключается в том, чтобы найти текущую стоимость на текущую дату (при t = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости (см. CFA — Эквивалентность приведенной и будущей стоимости денежных потоков).

Как показано на временной лини, мы можем рассматривать сумму при t = 9 в качестве будущей стоимости с точки зрения t = 0.

Мы вычислим текущую стоимость (PV) при t = 0 следующим образом:

FVN = €15,372,451.03 (текущая стоимость при t = 9)
N = 9
r = 5% = 0.05

PV = FVN * (1 + r)-N
= €15,372,451.03 * (1.05)-9
= €15,372,451.03 * (0.644609)
= €9,909,219.00

Приведенная стоимость на текущую дату (при t = 0) пенсионного обязательства составляет €9,909,219.00.

Приведенный пример иллюстрирует три процедуры:

• определение текущей (PV) или будущей стоимости (FV) любой последовательности денежных потоков;
• признание эквивалентности текущей и будущей стоимости; а также
• отслеживание фактического календарного времени на временной шкале при вычислениях, связанных с временной стоимостью денег (TVM).

Как вычислять текущую стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?

Рассмотрим случай обычного аннуитета, который продолжается бесконечно. Такой обычный аннуитет называется бессрочным аннуитетом или перпетуитетом или вечной рентой (англ. ‘perpetuity’ или ‘perpetual annuity’).

Чтобы получить формулу для текущей стоимости перпетуитета, мы можем модифицировать формулу 10, чтобы учесть бесконечную последовательность денежных потоков:

\( \mathbf {PV = A \sum _{t = 1} ^{\infty} \left } \) (формула 12)

Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:

PV = A / r (формула 13)

Чтобы понять смысл этого преобразования, обратите внимание на формулу (11) текущей стоимости обычного аннуитета.

Поскольку N (количество периодов в аннуитете) переходит на бесконечность, выражение 1 / (1 + r)N приближается к 0, а формула 11 упрощается до формулы 13.

Эта формула потребуется, когда мы будем оценивать дивиденды от акций, поскольку акции не имеют предопределенного срока действия.

Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.

При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.

Формула 13 справедлива только для бессрочного аннуитета с равными платежами. В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.

Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.

Пример расчета текущей стоимости (PV) перпетуитета.

Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.

Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?

Решение:

Чтобы ответить на этот вопрос, мы можем использовать формулу 13 со следующими данными:

A = £100
r = 5% = 0.05

PV = A/r
= £100/0.05
= £2,000

Облигация будет стоить £2 000.

Текущая стоимость на момент времени, отличный от текущей даты (t = 0).

На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от t = 0.

Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.

По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.

Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.

Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.

Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при t = 5.

Какова будет его текущая стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?

Решение:

Во-первых, мы находим текущую стоимость перпетуитета при t = 4, а затем дисконтируем эту сумму к текущей дате t = 0. (Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс t = 4 для нашего расчета текущей стоимости).

1. Находим текущую стоимость перпетуитета при t = 4:

A = £100
r = 5% = 0.05

PV = A/r
= £100/0.05
= £2,000

2. Находим текущую стоимость будущего значения при
t = 4.

С точки зрения сегодняшней даты t = 0 текущую стоимость в £2,000 можно считать будущей стоимостью.

Теперь нам нужно найти текущую стоимость £2,000 при
t = 0:

FVN = £2,000 (текущая стоимость при t = 4)
r = 5% = 0.05
N = 4

PV = FVN * (1 + r)-N
= £2,000 * (1.05)-4
= £2,000 * (0.822702)
= £1,645.40

Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.

Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.

В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при t = 5; после этого платежи продолжаются бесконечно.

Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к t = 5.

Благодаря этому перпетуитет с отсроченной 1-й выплатой (до t = 5) обеспечивает выплаты при t = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.

Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.

Следующий пример иллюстрирует этот результат.

Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.

С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:

Решение:

Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при t = 1, 2, 3, 4).

Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:

PV0 (Перпетуитет 1) = £100 / 0.05 = £2,000
PV4 (Перпетуитет 2) = £100 / 0.05 = £2,000
PV0 (Перпетуитет 2) = £2,000 / (1.05)4 = £1,645.40

PV0 (Аннуитет)
= PV0 (Перпетуитет 1) — PV0 (Перпетуитет 2)
= £2,000 — £1,645.40
= £354.60

Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.

Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?

Когда мы имеем неравные денежные потоки, мы должны сначала найти текущую стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.

Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.

В таблице ниже приведена последовательность денежных потоков с

• временными периодами в 1-м столбце,
• денежными потоками во 2-м столбце и
• текущей стоимостью (PV) каждого денежного потока в 3-м столбце.

В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.

Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.

Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.

Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду t = 5:

Введем следующие обозначения:

PV — текущая стоимость;

г — процентная ставка дисконта;

t — количество лет;

FVt — будущий доход, который ожидается получить через t лет;

dt- коэффициент дисконтирования;

Ро — текущая стоимость обыкновенной акции.

Тогда:

PV = F Vt dt;

PV= FVt e — непрерывное дисконтирование;

т PV = X FV dt (FVt — суммы, которые выплачиваются в t — м промежутке

t=i * в будущем);

PV = FV/r — текущая стоимость пожизненного дохода, если каждый год будут выплачиваться постоянные суммы FV.

Последняя формула получена с помощью суммы бесконечно убывающей прогрессии

PV=FVi FV i FV i =1 + г = FV = FV

1+r (1 + r)10 (1 + r)3 «‘ i___L (цт{1+т-1) r ‘

1+r v\ 1+r

Po = D/r — текущая стоимость акции с постоянными в будущем дивидендами D.

t=tl (1 + r)1

— текущая стоимость акции, дивиденды по которой начинают выплачивать с периода ti до бесконечности (Dt — ожидаемые дивиденды в конце t — го перио-

Di(l+g) да). На практике пользуются приближенной формулой Р0 =———, закладывая постоянный рост будущих дивидендов g.

Цена не пожизненной акции находится по формуле

l=7+(l + r)2+ (l + r)3+'»(l + r)n+ (l + r)n

Здесь

I — постоянный годовой процент в гривнах, г — соответствующая ставка процента для выпуска облигации, М — номинал или стоимость погашения акции через п лет (в конце периода),

п — число лет до погашения облигации.

Внутренняя норма доходности IRR — это процентная ставка, при которой современная стоимость рассматриваемого инвестиционного проекта равна нулю. Она определяется решением уравнения

NPV = Уг—г = 0.

Здесь

NPV- чистая современная стоимость; Т — количество лет;

CFt — чистый поток доходов в t -ом году (чистый поток денежных средств — это разница между ожидаемыми поступлениями за определенный период и расходами).

На основе анализа г = IRR, CFt устанавливают, убыточным или неубыточным будет проект. IRR надо находить с помощью EXCEL (финансовые функции).

Начисление по вкладам может производиться по простым и по сложным процентам

Sn=P(l+ni)- для простых процентов,

Sn=P(l+i)n — для сложных процентов.

Sn — величина вклада Р через п лет при годовой ставке i.

Графическая иллюстрация соотношения сумм, наращиваемых по любому, в том числе дробному строку t > О приведена на рис. 5.1.

Рис 5.1

С рисунка видно, что при срочности t < 1 начисления по простым процентам превышает сложный процент; при переходе через единичный промежуток картина меняется: превалирует сложный процент, причем с возрастающей во времени отдачей. Например

(l+i)1/2<l+-i

и

(1 + i)2 > 1 + 2i.

Учет инфляции производится по формуле

S = P, где 1 + г

S — наращенная сумма через год; Р — вложенная сумма; i — процентная ставка; г — годовой темп инфляции. Реальная ставка процента ir находится по формуле 1

При достаточно большом г реальная ставка процента ir может стать даже отрицательной. Отсюда видно, что, если кредитор не отреагирует на инфляцию достаточным увеличением ставки, он будет работать себе в убыток, а заемщик при этом будет обогащаться. Если

р = 1+ г — индекс цен (рост цены),

то инфляция означает рост цен

р = 1 + г.

Поэтому, чтобы получить реальную ставку i с учетом инфляции, надо требовать наращенную ставку

j = i + r + ir .

Тогда реальная ставка

ir =(i + г + ir — г)/(1 + г)= 1.

При невысокой инфляции величины i и г незначительны, и их произведением в формуле можно пренебречь. В этом случае поправка на инфляцию ограничивается величиной темпа г, и ставку корректируют по формуле

j = i + г.

Процентная ставка, скорректированная с учетом риска, равна

mi = r0 + Pi (me — г0). Дисконтируя по этой ставке, получим оценку текущей стоимости:

1 + г0+а{(тс -г0)

Ро _Т.——Г^7———Т> гДе

Д1 — дивиденды.

Другие параметры будут объяснены при рассмотрении модели САРМ. Для расчета базисной требуемой нормы прибыли от акционерного капитала (процента) используют такие основные методы:

1. САРМ;

2. Прибыль компании от облигаций плюс вычисленная премия за риск;

3. Дивиденды плюс вычисленные темпы роста;

4. Модель APT.

В зависимости от дополнительного процента (премия за риск), кото рый надеются дополнительно получить инвесторы сверх гарантированного, определяется характер рискованности проекта (табл. 5.1).

Таблица 5.1

Характер проекта	Премия за риск, %
Низкорискованный
Среднерискованный
Высокорискованный

Чем выше степень рискованности проекта (выше премия за риск), тем больший знаменатель в формуле для Р0 и соответственно меньшая приведенная стоимость проекта.

При определении текущей стоимости капитала основным является понятие дисконта. Как уже отмечалось, коэффициент дисконтирования является нормативом приведения разновременных затрат к единому моменту. При назначении коэффициента дисконтирования обычно ориентируются на существующий или ожидаемый усредненный уровень ссудного процента и субъективные оценки, основанные на опыте инвестора. Важным моментом при определении процентной ставки, применяемой при дисконтировании, является учет риска.

Пример 5.1. Предприниматель взял 2 тыс. гривен в банке под 50% годовых. Сколько денег ему придется вернуть через 5 лет?

Решение. Р = 2000, Т = 5, г = 0,5. Следовательно, FV5 = 2000(1+0,5)5 = =15 187,41 (гривен).

Пример 5.2. Что полезней: получить сразу 5 тыс. гривен или получать ежегодно 1200 на протяжении 5 лет при условии, что годовая процентная ставка составляет 10%?

Решение. Подсчитаем текущую цену денежных поступлений.

1200 1200 1200 1200 _J2Q0_ (1+0Д)1+(1+0,1)2+(1+0,1)3+(1+0,1)4+(1+0,1)5 -4548’94

Следовательно, лучше получить 5 тыс. гривен сразу, чем получать 5 лет по 1200 гривен.

Пример 5.3. Определить, сколько стоит сейчас 1 доллар при процентной ставке 2, 6, 10, 20% через 1, 2, 5, 10, 20, 30 лет.

Результаты вычислений занесены в табл. 5.2.

Таблица 5.2

Существенный качественный скачок происходит при процентной ставке, равной 6-7%. Если вложить 3 цента под 20% годовых, то через 20 лет они превратятся в доллар. Кстати, годовая инфляция доллара равна около 4,3%.

В финансовом деле процентные ставки часто обозначают буквами: г, i, К, k, Kd, Kd, g, Rf, Kr, чтобы отличать смысл каждой процентной ставки. Для удобства вычислений составлены таблицы по которым можно легко определять текущую и будущую стоимости денежных поступлений. Приведем здесь четыре основные табл. (5.3-5.6).

Сложная (будущая) стоимость 1 гривны. CVIF(K,n) (compound value interest factor)

CVIFk,n = (l + K)n

Таблица 5.3

Сумма ежегодного дохода в одну гривну в течение п периодов. CVIFA(K,n) (compound value interest factor annuity)

CVIFA= X(l + K)n-t =X(1 + K)t_1

Таблица 5.4

Текущая стоимость 1 гривны. PVIF(K,n) (the present compound value interest factor)

PVIFK,n =1/(1 + K)n

Таблица 5.5

Текущая стоимость ежегодной ренты в одну гривну. PVIFA(K,n) (the present compound value interest factor annuity)

PVIFAK,n = y(n i)/it(i+K)1

Таблица 5.6

Пример 5.4. Вам предложили десятилетний 9%-ый купон облигации номиналом в 1000 гривен по цене 1066 гривны. Какую ставку процента вы бы заработали, если бы купили акцию и держали ее до погашения.

Чтобы найти прибыль до погашения, необходимо решить уравнение относительно К:

Лпгг90 90 90 1000

1066 = (1 + К) (1 + К)2 (1 + К)10 (1 + К)10

или

PVIFA(0,9,10)=6,418, PVIF(0,9,10)=0,433 90-PVIFA(0,9,10)+1000-PVIF(0,9,10)=90-6,418+1000-0,433=1010,62<1066. Возьмем К=8%.

Пример 5.5. Фирма рассматривает целесообразность реализации двух проектов А и Б. Ожидаемые потоки доходов CFt приведены в табл. 5.7.

Таблица 5.7

	Годы
Проект A (CFt)
Проект Б (CFt)

Примечание. Отрицательная величина означает расходы. Определить:

1) внутреннюю норму дохода;

2) период окупаемости;

3) современную стоимость денежных поступлений при норме дисконта с учетом риска и инфляции равной 20%.

Решение.

1. Для проекта A IRR А находится решением уравнения

-2500 2000 1000 900

(l + IRRA})+(l + IRRA)1+(l + IRRA)2+(l + IRRA)3

Решая это уравнение, находим IRRA=31,3%.

Для проекта Б IRR Б находится решением уравнения

-2500 900 1000 2000

(l + IRR f (l + IRR } (l + IRR } (l + IRR f

Решая это уравнение, находим IRRB=22,4%.

Так как IRRa >IRRb, to относительно кредитования более привлекательный проект А.

2. Период окупаемости — это количество лет, которые необходимы для компенсации средств, вложенных в реализацию проекта, доходами, полученным за период его эксплуатации.

Периоды окупаемости можно находить без учета дисконтирования и с учетом дисконтирования денежных потоков.

1) Определим период окупаемости без учета дисконтирования (табл. 5.8).

Таблица 5.8

	Аккумулированные потоки по годам
Проект А
Проект Б

где

Период окупаемости проекта А равен Т = 1 ч——-= 1,5(года).

Период окупаемости проекта Б равен Т = 2 ч———= 1,3(года).

2) Определим период окупаемости с учетом дисконтирования. Период окупаемости с учетом дисконтирования находится по формуле

Т = тч-S-CF(1 + г)

1о — вложенные средства;

S = У-Ц и находят так, чтобы Sm< Io< Sm+i.

m Й(1ч-г)1

Вычисления оформляем табл. 5.9.

Таблица 5.9

Год	Проект А		Проект Б
	Годовой дисконтированный поток	Аккумулированный поток	Годовой дисконтированный поток	Аккумулированный поток
0 1 2 3	-2500 1818 909 744	-2500 -682 227 971	-2500 818 909 1653	-2500 -1682 -773 880

Следовательно

Т =1ч- —= 1,75(года), а 909

Т = 2 + ^- = 2,47(года). Б 1653 V}